|
> Accueil > Campus de Metz > Recherche > Photonique@SUPELEC
Auto-organisation de la lumière L’effet photoréfractif est un effet non linéaire consistant en la modification locale de l’indice de réfraction d’un milieu due à une illumination. Si un faisceau laser unique est envoyé sur la face d’entrée du matériau, par effet Pockels correctement polarisé, il apparaît une augmentation locale de l’indice de réfraction, donc un effet d’autoguidage du faisceau. Cette autofocalisation peut être stable et compenser exactement la diffraction naturelle : le faisceau ne diffracte plus et on peut le qualifier de « soliton spatial ». Si l’ illumination est périodique, un réseau d’indice est créé dans le cristal photoréfractif, via un phénomène de mélange d’ondes (Two Wave Mixing). Dans une configuration de faisceaux contra-propageants, le faisceaux laser incident peut devenir instable via un phénomène d’Instabilités de Modulation et la formation de structures spatiales auto-organisées dites « patterns » peut être observée. Inscription photoréfractive de guides dans InP :Fe
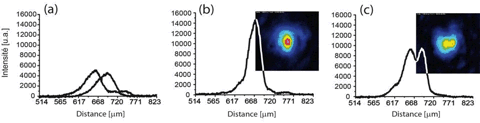
Ces travaux ont pour objectif les communications optiques et, plus précisément, le routage optique. En effet, la réalisation de réseaux tout optiques ne nécessitant pas l’intervention d’éléments électroniques pour la détection temporaire des signaux demande des éléments de routage et d’interconnexion optique, adaptables et reconfigurables en des temps courts. Dans ce but, nous étudions l’autofocalisation dans des matériaux photoréfractifs semi-conducteurs (InP :Fe) de part leur sensibilité aux longueurs d’onde IR et leur temps de réponse court. Nous avons ainsi montrer la possibilité pour un faisceau laser IR d’être autofocalisé en quelquesdizaines de microsecondes.
Nous étudions l’évolution du taux d’autofocalisation en fonction de différents paramètres (intensité, température, dopage). Des études expérimentales en cours concernant l’évolution transitoire de l’autofocalisation photoréfractive dans InP :Fe et dans un nouveau matériau photoréfractif, SPS, à deux longueurs d’onde (1064 et 1550 nm). Références principales : Interactions de solitons
Nous étudions, à la fois expérimentalement et théoriquement, les interactions de solitons co ou contra-propageant dans les semi-conducteurs photoréfractifs. Nos études ont démarrer par l’interaction entre deux solitons parallèles ou inclinés et nous avons pu déterminer la distance minimale de non interaction : nous étudions ainsi le comportement de jonctions X ou Y, réalisées entre deux guides voisins se repoussant ou se fusionnant. La maîtrise et le contrôle de ces interactions de solitons est un processus essentiel utile dans des dispositifs photoniques 3D basés sur des matrices de guides solitons adressables et reconfigurables.
Références principales : Patterns optiques et solitons de cavité
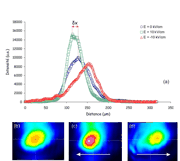
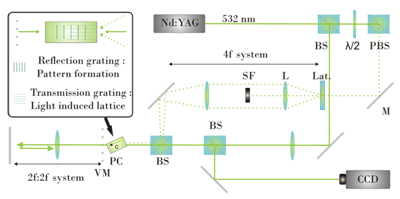
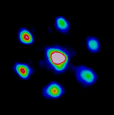
La possibilité de former spontanément une structure spatiale régulière (pattern) à partir d’un état spatial homogène a été initialement introduite par A. Turing. Ce mécanisme dit d’instabilité de modulation permettant la formation de ces structures spatiales auto-organisées a été depuis démontré expérimentalement dans de nombreux systèmes photoniques comportant comme milieu optique non-linéaire des vapeurs atomiques, cristaux liquides, films organiques ou encore matériaux photoréfractifs. Nous nous intéressons plus particulièrmeent au contrôle de pattern optique dans un cristal photorfércatif soumis à une rétrocation optique (simple feedback).
Nous nous sommes intéressés plus spécifiquement à des techniques de contrôle du seuil d’instabilité de modulation conduisant au pattern, par exemple en combinant la cavité photoréfractive avec un cristal photonique, ou en modifiant la position et l’angle du miroir induisant la rétro-action. Références principales : |
|||||||||||||||||||