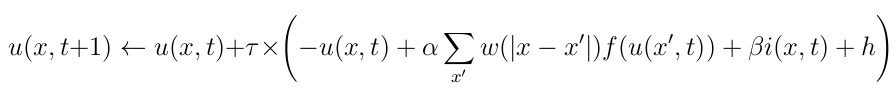Champs neuronnaux dynamiques

par Hervé Frezza-Buet.

Prise en main

Dans ce tp, on vous fournit une bibliothèque pour mettre en oeuvre facilement des champs neuronnaux dynamiques. Il s'agit de deux fichiers python, filtering.py et field.py, que voud devrez télécharger. Pour apprendre à utiliser cette bibliothèque, regardez les parties "main" de chaque fichier. Vous pourrez lancer les exécutions correspondantes par 
python filtering.py
puis 
python field.py
A titre d'exemple, regarder comment on peut facilement implémenter le jeu de la vie de Conway : game_of_life.py

Instabilités de Turing

Programmez un champ 640x480 dont l'équation de chaque unité est la suivante. Pour une unité x d'activité u(x), on note v(x) la somme des activités des unités x' telles que 10 ≤ d(x,x') ≤ 50. Soit un seuil s arbitraire. L'évolution de l'activité de u(x) est alors: Vous pourrez initialisez le champ avec des valeurs u(x) aléatoires dans [0,1]. Que se passe-t-il pour s=1000 ? pour s=3850 ?

Champs neuronaux pour l'attention

Nous utiliserons un champ neuronal défini par l'équation suivante :

On choisira

w(r) = (1+g)*exp(-r²/2σ²) - g

Pour la simulation, on discrétisera par une méthode d'Euler comme suit :

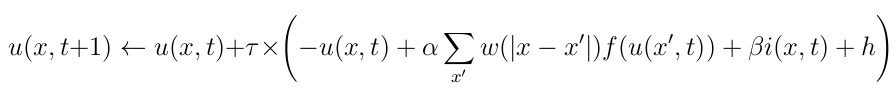
Attention On maintiendra au cours du temps les valeurs de u dans [0,1]. On choisira dans un premier temps les valeurs suivantes des paramètres : g=.5, σ=12, τ=0.3, α=0.005, β=1, h=-0.5. La fonction f est une non linéarité. On pourra prendre l'identité dans un premier temps, pour annuler son effet. Regardez comment le champ neuronal réalise la sélectiion d'un point d'attention en complétant le code donné dans dnf-skeleton.py. Vous pouvez exécuter ce script avant de le modifier.

Champs neuronaux pour l'auto-organisation

Créez deux nouveaux champs omega_x et omega_y, initialisée aléatoirement entre -1 et 1. Tous les 50 pas de temps, tirez une valeur ξ dans le cercle unité. Construire alors le champ i qui donne la valeur de matching de chaque prototype (omega_x,omega_y) avec ξ et mettez en place un apprentissage des prototypes de type Kohonen, qui soit modulé par l'activité u calculée sur la base de i.

L'architecture est résumée par le figure ci-dessous:

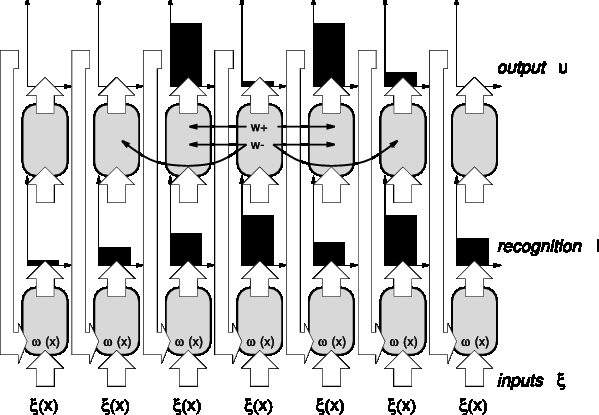
Observe-t-on une auto-organisation ? Pour répondre à cette question, sachez que le profile de la distribution i en réponse à un exemple ξ doit évoluer comme sur la figure ci-dessous au cours du temps.

































. .
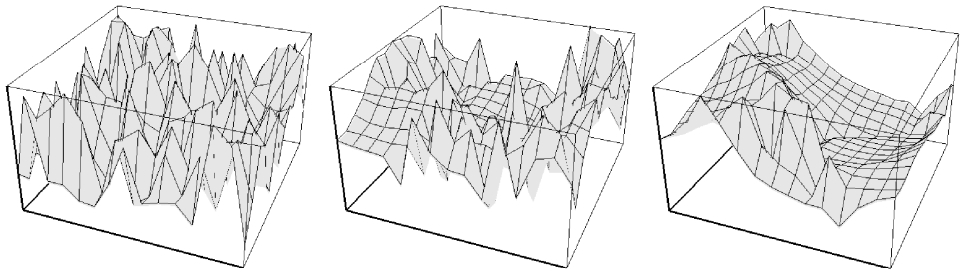