Situated cortical computation
I am a member of the Information, multimodality and Signal team of Supélec and UMI 2958 Georgia Tech / CNRS.
High performance computing for large scale fine grain dynamical systems using InterCell
The booz library allows to implement large scale dynamical systems made of populations of inter-connected units. Such systems can run on the InterCell cluster.
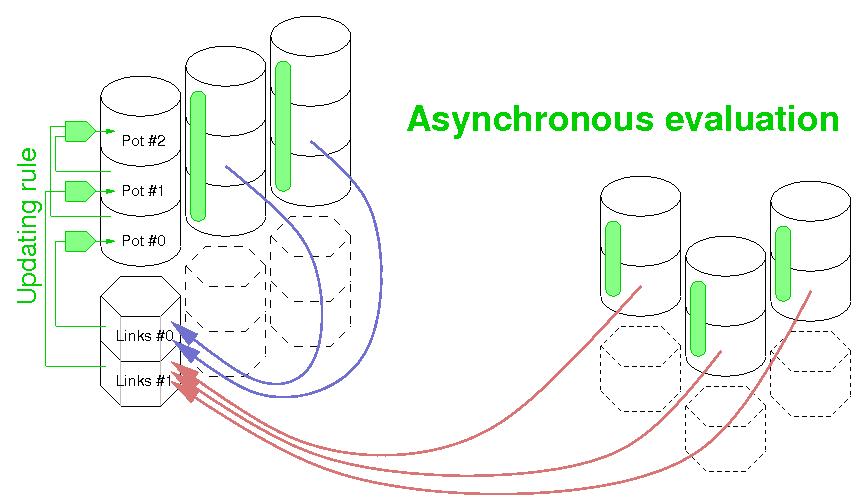

Demos
This is a grid network spring-mass system designed with booz and visualized with booz vizualization tools. Within the lens, the mass is a slightly heavier.
This is the resolution of some differential equation with intercell. You can see the guiding of some laser beam in a guide... ok, ask Nicolas Fressengeas for details.
The bijama model
The bijama model is a way to design neural system with a "cortical flavour". It is based on neural fields, that are coupled through inter-map connections, and that compute a distributed decision process. The decision selects which action has to be done when it occurs in motor maps, but more generally, the decision between each module aims at selecting some reduced patch of units where learning occurs.
The model addresses multi-modal self-organization in a fully distributed competitive architecture.
O. MÉNARD, H. FREZZA-BUET, "Model of multi-modal cortical processing: Coherent learning in self-organizing modules". In Neural Networks, 18(5-6):646-655, 2005
The picture below shows what connection strips are in the bijama model, and this movie shows their dynamical effect when they are used to couple several neural fields.
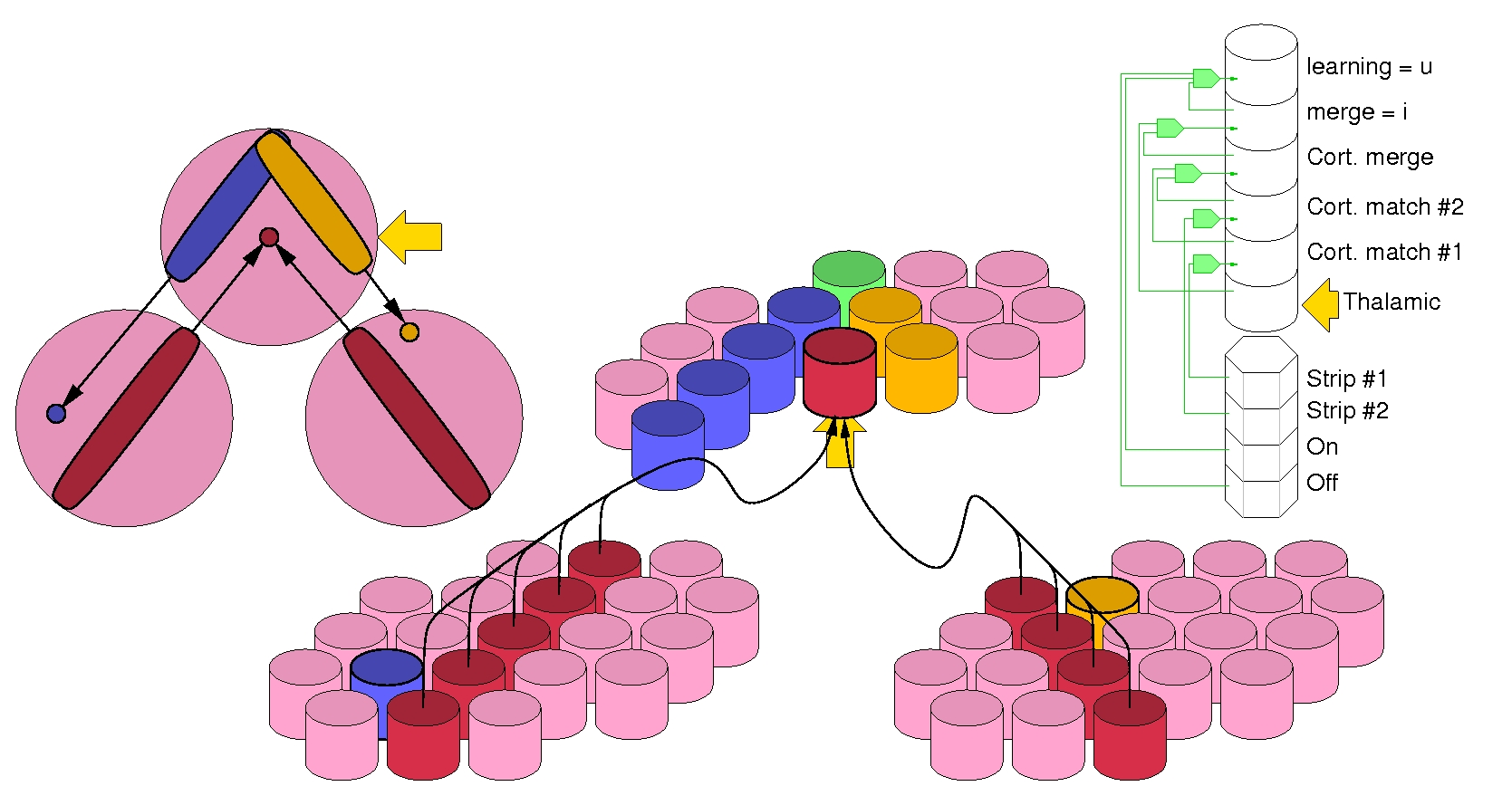

In such architectures, the core computation is the self-organizing process that drives the learning in each map. It is based on some neural field like competition system. Driving self-organization with neural field is not straightforward, since many side effects appear when dealing with a fully distributed dynamical process for such purpose.
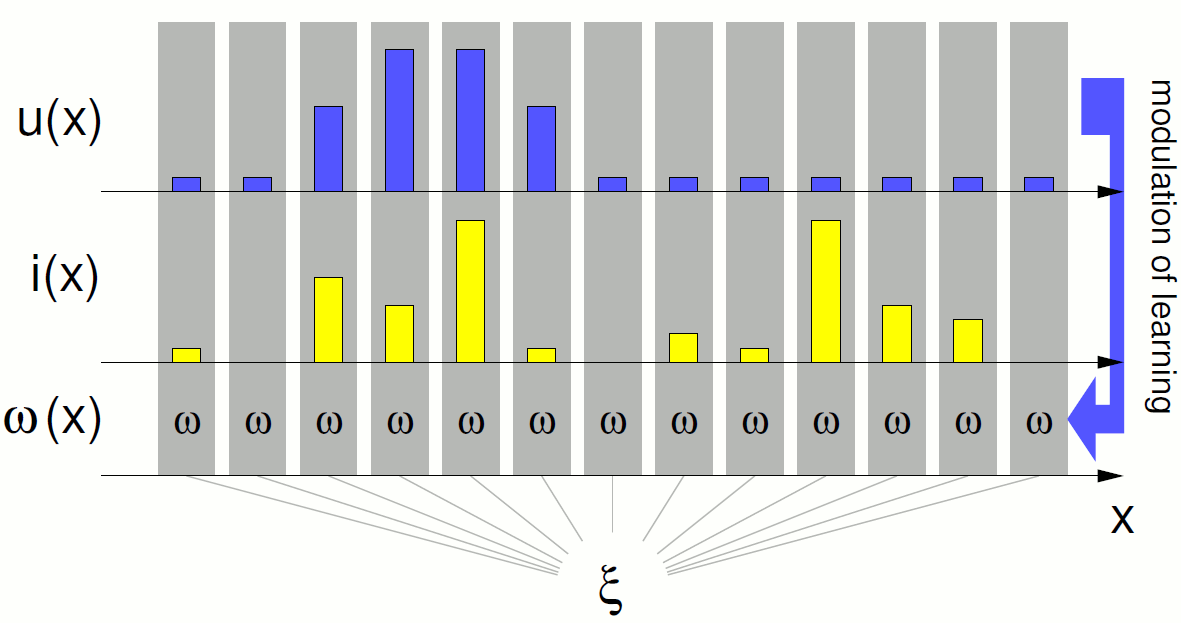
When random colors are presented to such a map, prototypes omega get organized as this. The u and i distribution profile evoluate like this. The smoothing of the i profile as the map gets organized is a change in the dynamics that the neural field has to cope with.
L. ALECU, H. FREZZA-BUET, F. ALEXANDRE, "Can self-organization emerge through dynamic neural fields computation? ". In Connection Science, 23(1):1-31, 2011
Since we know how to drive self-organization in bijama, we have set up a recurrent architecture in order to deal with ambiguous temporal sequences. The sequence elements are numbers in [0,1], represented by letters from A to F, A being black and F being white. The results can be found in the following paper.
B. KHOUZAM, H. FREZZA-BUET, "Distributed Recurrent Self-Organization for Tracking the State of Non-Stationary Partially Observable Dynamical Systems". In Biologically Inspired Cognitive Architectures, 3:87--104, 2013
The architecture is presented below, see the spatio-temporal self-organization as well as unexpected mapping instabilities.
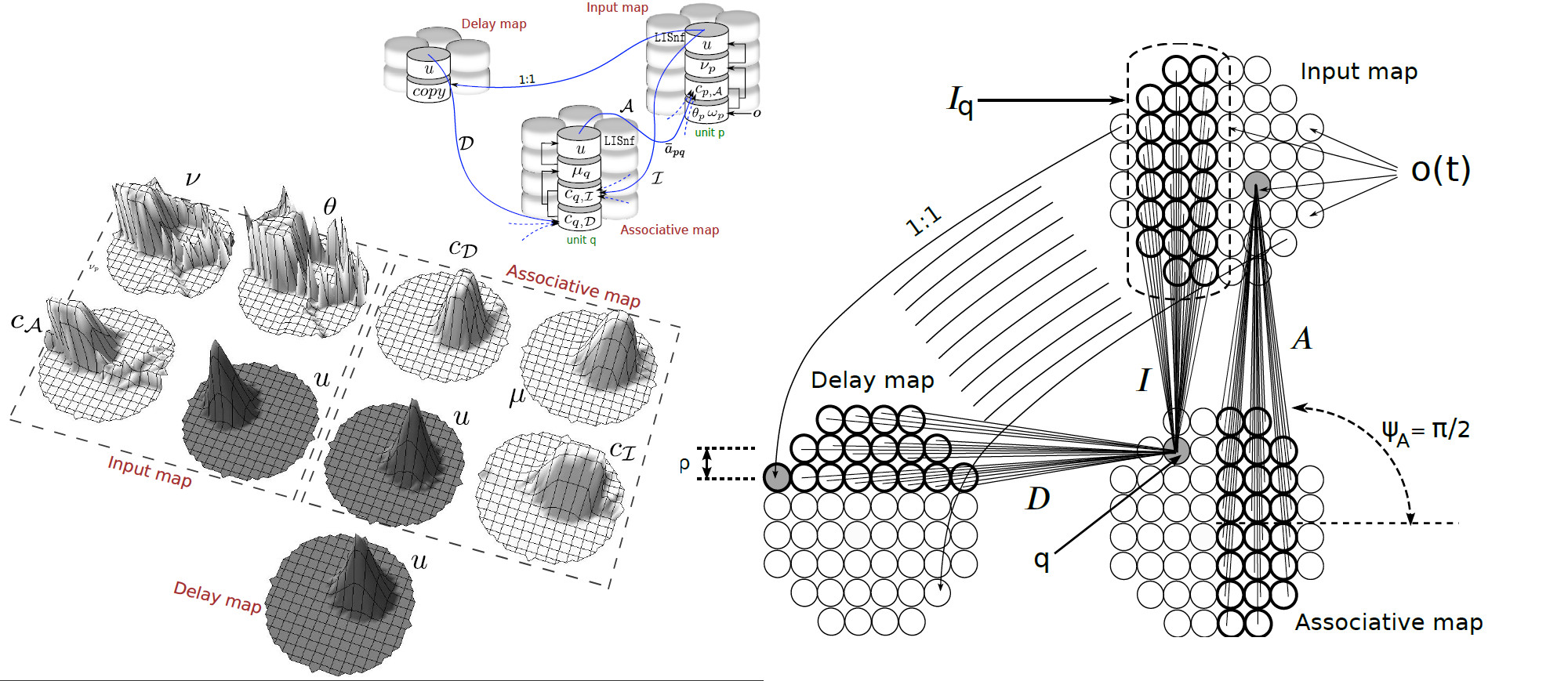
Related research
GNG-T : Self-organization on non-stationary distributions.
GNG-T is an extention of GNG by Fritzke that monitors the number of neurons according to some specified quantification accuracy (i.e. the target T). Recent work concerns the stabilization of the prototype position and a velocity field extraction that is robust to the aperture problem.
You can use the GNG-T algorithm since I provide a library for that. Watch the videos on that page !
H. FREZZA-BUET, "Following non-stationary distributions by controlling the vector quantization accuracy of a growing neural gas network". In Neurocomputing, 71(7-9):1191-1202, 2008
H. FREZZA-BUET, "Online computing of non-stationary distributions velocity fields by an accuracy controlled growing neural gas". In Neural Networks, 60:203-221, 2014