Vie artificielle : Calculer avec des neurones à Spikes
Table des matières
Introduction
L'idée de ce TP est d'utiliser des neurones à Spikes pour faire des calculs. Les modèles de neurones à Spikes produisent des trains d'impulsions (les spikes) qui sont échangés entre les neurones et on cherche ici à montrer qu'en connectant des neurones à Spikes entre eux de façon appropriée (voire apprise), on peut calculer des choses intéressantes.
Les simulations se feront à l'aide du simulateur Python3 Brian2
On trouvera dans la section Annexe de cette page différents bouts de code Python/Brian qui seront utiles pendant le TP.
Présentation du problème
On s'intéresse dans ce TP à construire des réseaux de neurones à spikes capables de reconnaitre des séquences spatio-temporelles. Le problème qu'on considère est celui de la reconnaissance de la parole et est basé sur une compétition lancée en 2000 par J.J. Hopfield et C.D. Brody. Ils proposaient dans un papier intitulé "What is a moment ? Cortical sensory integration over a brief interval" des enregistrements simulés de neurones d'un animal imaginaire reconnaissant des signaux de parole. Ils ne fournissaient aucune indication sur la structure du modèle qui a permis de les générer et proposaient comme compétition de produire des réseaux de neurones à spikes capable de générer ces données.
Ce problème de détection de motifs spatio-temporels pourraient évidemment être résolu avec d'autres techniques de Machine Learning. Pour rester dans le thème des réseaux de neurone, on pourrait tout à fait utiliser des réseaux feedforward avec fenêtre de temps glissante ou bien des réseaux récurrents de type LSTM. L'objet ici est avant tout d'explorer une autre façon de calculer, en utilisant des neurones à Spikes. Ce calcul repose sur l'échange d'une information beaucoup plus pauvre qu'un potentiel (un double) dans le cas des réseaux de neurones plus conventionnel. Les neurones ne signalent que des événements, un bit de temps à autre. Et on va voir dans ce temps comment on peut jouer avec ce type d'unité très pauvre pour commencer à résoudre un problème de détection de motifs spatio-temporels.
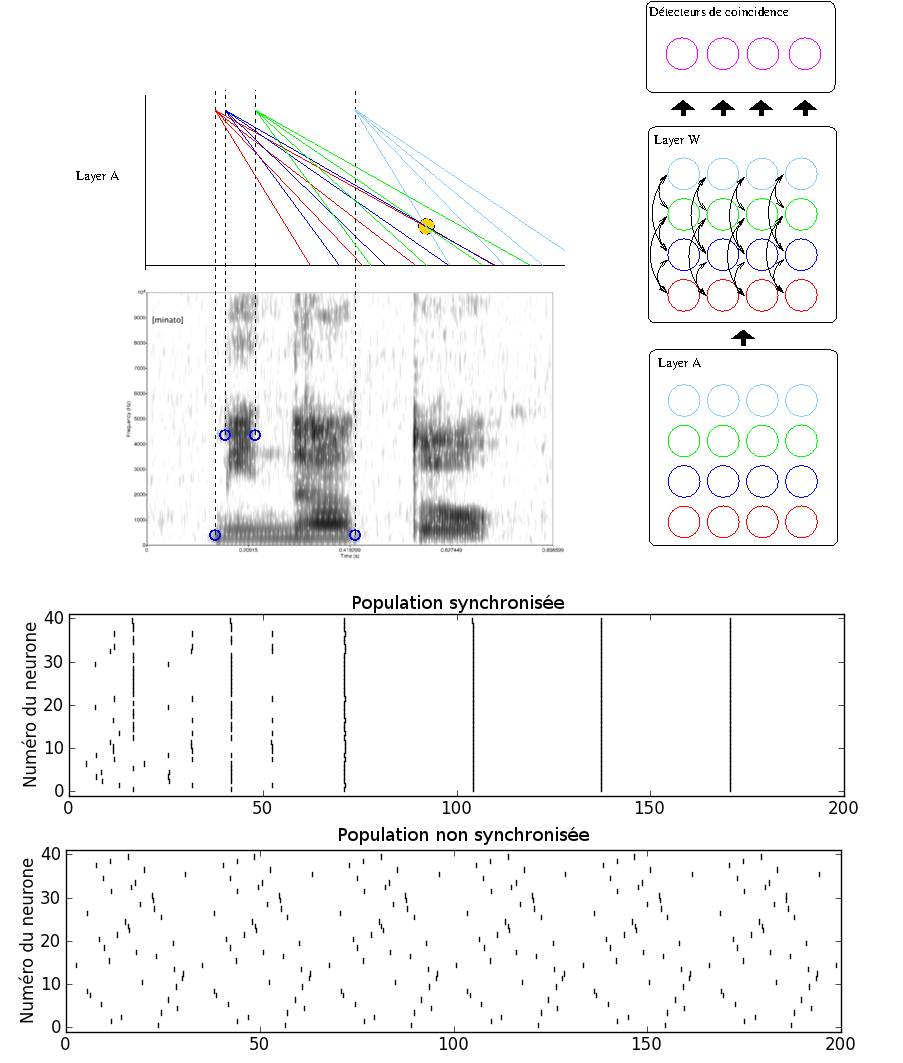
Le modèle est construit sur 3 couches. La couche A est remplie de neurones détectant des événéments particuliers d'un spectrogramme, comme l'apparition de réponse dans une bande de fréquence particulière. En réponse à ces événements, plusieurs neurones vont émettre des spikes (des impulsions) à des fréquences décroissantes à partir du moment ou l'événément a été détecté. Il arrive que pour une séquence particulière d'événements, un sous ensemble des neurones de la couche A vont répondre avec une fréquence de décharge proche (ce qu'on a représenté par le cercle jaune). Comme on le verra, les neurones peuvent répondre avec une fréquence identique mais pas forcément en phase. Dans la couche W, les neurones sont couplés et on va voir que ce couplage permet d'amener les neurones à décharger en phase. Une fois que ces neurones déchargent en phase, on peut définir des neurones qui détectent cette coincidence pour décider qu'une séquence particulière est détectée.
On va progressivement construire le réseau qui permet de résoudre le problème de reconnaissance de parole ci-dessus. Les briques élémentaires dont on a besoin sont :
- montrer que la fréquence de décharge d'un intégrateur à fuite dépend du courant injecté
- montrer qu'une population de neurones à spikes faiblement couplés et déchargeant à une fréquence proche se synchronisent de manière transitoire
- détecter la coincidence de spikes (la synchronisation transitoire)
Prise en main de Brian
Installation de Brian
Les machines de Supélec disposent déjà de tout les paquets installés
Sinon : BrianInstallation
Mes premiers spikes en Brian
Brian est une librairie Python. Python est un langage de script assez rapide à prendre en main (sachez qu'on peut y faire des choses compliquées avec des objets etc... qu'on ne verra pas explicitement ici; dans ce TP, on passera uniquement par la définition et l'appel de fonctions) et autour duquel il existe plein de librairies qui permettent de faire du calcul de scientifique (numpy), des illustrations (matplotlib), du traitement d'image (PIL), du calcul symbolique (sympy), etc...
Un script Brian2 contiendra des commandes pour :
- importer la librairie Brian
- définir les paramètres et les équations d'un modèle (cf Models)
- créer des populations de neurones (grâce à l'objet NeuronGroup)
- connecter des neurones entre eux (grâce à l'objet Synapses)
- spécificier des variables à enregistrer (grâce aux objets SpikeMonitor et StateMonitor, cf Monitor)
- spécifier des entrées externes au modèle (cf Input)
- lancer la simulation (par un appel à run, cf Running)
- visualiser/analyser les résultats
On peut également lancer en Brian des simulations intéractives mais on ne le fera pas ici. Un script tout simple en Brian aura donc la forme suivante :
Fichier ex1.py
# -*- coding: utf-8 -*-
from brian2 import *
defaultclock.dt = 0.01*msecond
tau = 20 * msecond # constant de temps
Vt = -55 * mvolt # seuil pour spiker
Vr = -75 * mvolt # potentiel de reset
Vs = -65 * mvolt # potentiel de repos
I0 = 15 * mvolt
tmax = 500 * msecond
# Notre groupe contient un neurone intègre et tire
eqs = '''
dV/dt = (-(V-Vs) + I)/tau : volt
I : volt
'''
G = NeuronGroup(N=1,
model=eqs,
threshold='V >= Vt',
reset='V = Vr',
method='linear')
# On monitore ses spikes et son potentiel
spikemon = SpikeMonitor(G)
statemon = StateMonitor(G, 'V', record=0)
# On initialise le potentiel aléatoirement entre le reset et le seuil
G.V = Vr + (Vt - Vr) * rand(len(G))
G.I = I0
# On lance la simulation
run(tmax)
# On affiche combien de spikes ont été émis
print("Nombre de spikes émis : ", spikemon.num_spikes)
print("Liste des temps de spikes :")
print(spikemon.spike_trains())
print(', '.join(["{} ".format(ts) for ts in spikemon.spike_trains()[0]]))
print("Temps inter-spikes (s.):")
print(', '.join(["{} ".format(t1-t0) for t0, t1 in zip(spikemon.spike_trains()[0][:-1], spikemon.spike_trains()[0][1:])]))
#### TODO
predicted_isi = 1 * second
print("Intervalle interspike {} ".format(predicted_isi))
print("Fréquence de décharge : {} ".format(1.0/(predicted_isi)))
####
# On trace nos mesures
figure()
subplot(211)
for i, ts in zip(spikemon.i, spikemon.t):
plot([ts/msecond, ts/msecond], [i, i+1], 'k')
ylim([-1,2])
xlabel("Temps (ms)")
ylabel(u"Numéro du neurone")
subplot(212)
plot(statemon.t, statemon.V.T)
ylabel('Potentiel (V)')
xlabel('Temps(s.)')
show()
Q1 - Sauvegardez le script précédent et exécutez le. Vous devriez voir quelque chose de la forme suivante:
bash:user$ python3 ex1.py
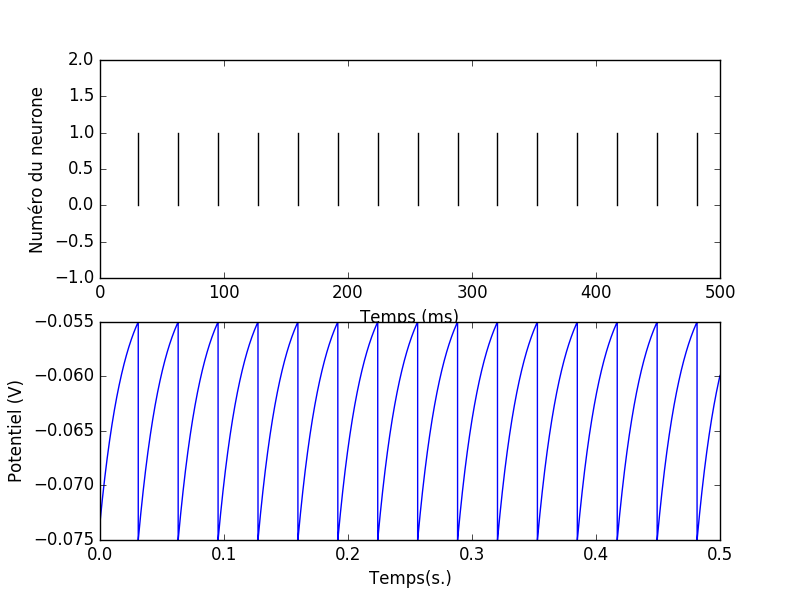
Comment marche le neurone ? On a commencé par initialiser son potentiel à un potentiel aléatoire entre le potentiel de reset et le potential de seuil. Brian se charge ensuite d'intégrer l'équation différentielle : τ(dV)/(dt) = − (V − Vs) + I. Lorsque le potentiel atteint le potentiel de décharge Vt = − 55mV, un spike est émis et le potentiel est réinitialisé au potentiel de reset Vr = − 75mV. On observe sur la figure du dessus les spikes émis par le neurone (représentés par les barres verticales) et l'évolution du potentiel de membrane.
Q2 - Prédire le temps des spikes : Dans la console, on affiche les temps d'émission des spikes et les temps inter-spikes. Calculez analytiquement les temps inter-spikes et vérifiez que ça colle avec la simulation étant donnés les paramètres de simulation. On peut alors en déduire la fréquence de décharge. On remarquera qu'en ignorant la latence du premier spike, le neurone décharge à une fréquence constante, dépendante du courant injecté. La latence du premier spike dépends du potentiel initial. Gardez l'expression que vous aurez trouvé, elle nous servira dans la partie sur les détecteurs de coïncidence.
Synchronisation de neurones à spikes
Maintenant qu'on sait simuler un neurone à spike intègre-et-tire, on va s'intéresser à ce qui se passe lorsqu'on considère une population de tels neurones et qu'on les connecte entre eux.
Une population de neurones à spikes
Q3 Inspirez vous du script précédent pour simuler une population de 40 neurones intègre et tire et afficher le raster plot (c'est le tracé des trains de spikes). On s'arangera pour que les potentiels initiaux des neurones soient fixés aléatoirement entre le potentiel de reset et le potentiel de décharge. On considéra les équations suivantes
τ(dV)/(dt) = − (V − Vs) + I0
si V ≥ Vt, alors V = Vr
avec les paramètres:τ = 20ms, Vt = − 55mV, Vr = − 75mV, Vs = − 65mV, I0 = 15mV. On exécutera la simulation pendant 200 ms.
Vous devriez observer (cf image ci-dessous) que les neurones déchargent à une fréquence constante mais avec des décalages de phase. On va voir qu'en couplant les neurones, on peut les amener à décharger de manière synchrone (même fréquence, même phase). Pour pouvoir afficher les potentiels de membrane de tous les neurones, il suffit de le préciser à la déclaration du StateMonitor :
StateMonitor(G, 'V', record=True)
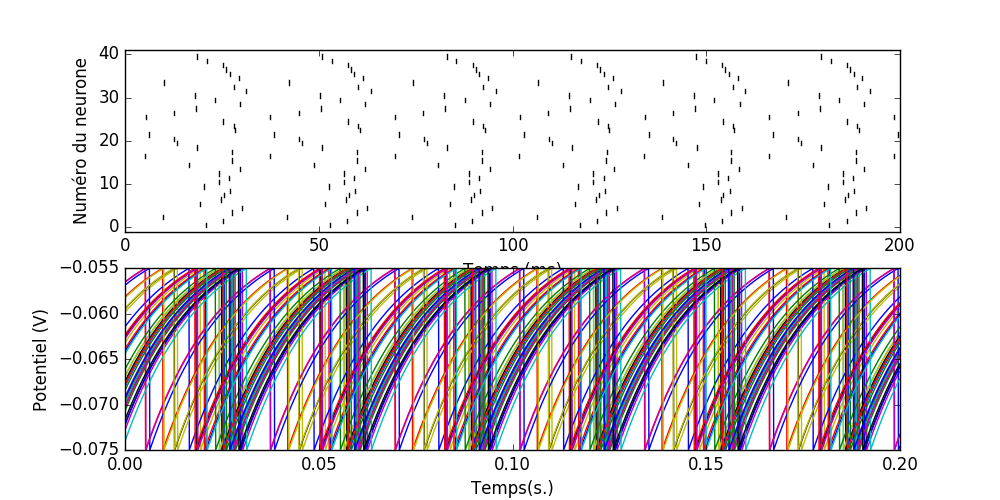
Une population de neurones à spikes faiblement couplés se synchronise
Q4 En partant de la simulation que vous venez d'écrire, couplez les neurones entre eux avec des connexions excitatrices de 0.2 mV ;
Se = Synapses(G, G, 'w : volt', on_pre='V_post += w') Se.connect(condition="i!=j") Se.w = 0.2 * mV
Le code ci-dessus, placé après la définition du groupe, connecte le groupe G à lui-même, sans qu'un neurone ne soit connecté à lui-même. Chaque fois qu'un neurone pré-synaptique émet un spike, la variable V du neurone post-synaptique est incrémentée de la valeur du poids, ici 0.2mv.
Q5 Vous pourrez essayer de varier le poids des couplages. Vous pourrez aussi essayer d'ajouter une période réfractaire (période pendant laquelle un spike pré-synaptique n'a aucune influence sur le neurone post-synaptique) aux neurones de 0.5ms, en le précisant dans la définition du groupe : "...,reset='V=Vr', refractory=0.5*msecond)". Vous devriez pouvoir synchroniser les neurones sans trop perturber leur fréquence décharge.
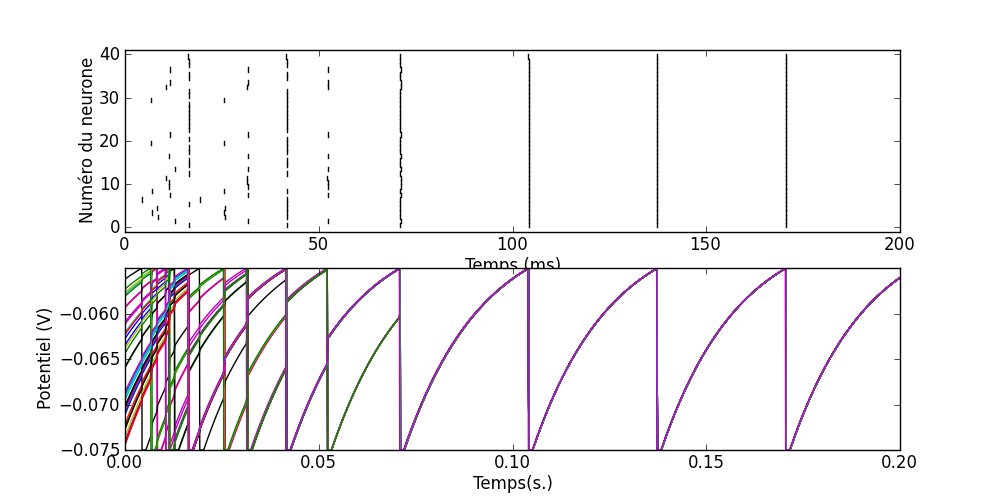
Synchronisation transitoire
On en arrive maintenant au type de synchronisation qui nous intéresse : la synchronisation transitoire. Dans le modèle de Hopfield, Brody, les neurones de la couche intermédiaire sont stimulés par des rampes décroissantes de courant. Chaque rampe décroissante de courant est déclenchée à la détection d'un attribut (un pique dans une bande de fréquence d'un spectrogramme d'un signal de parole par example). On souhaite que ces neurones se synchronisent lorsque leur courant d'entrée est proche puis se désynchronisent. Cette synchronisation transitoire pourra ensuite être détectée par des détecteurs de coïncidence (qu'on verra dans la prochaine section).
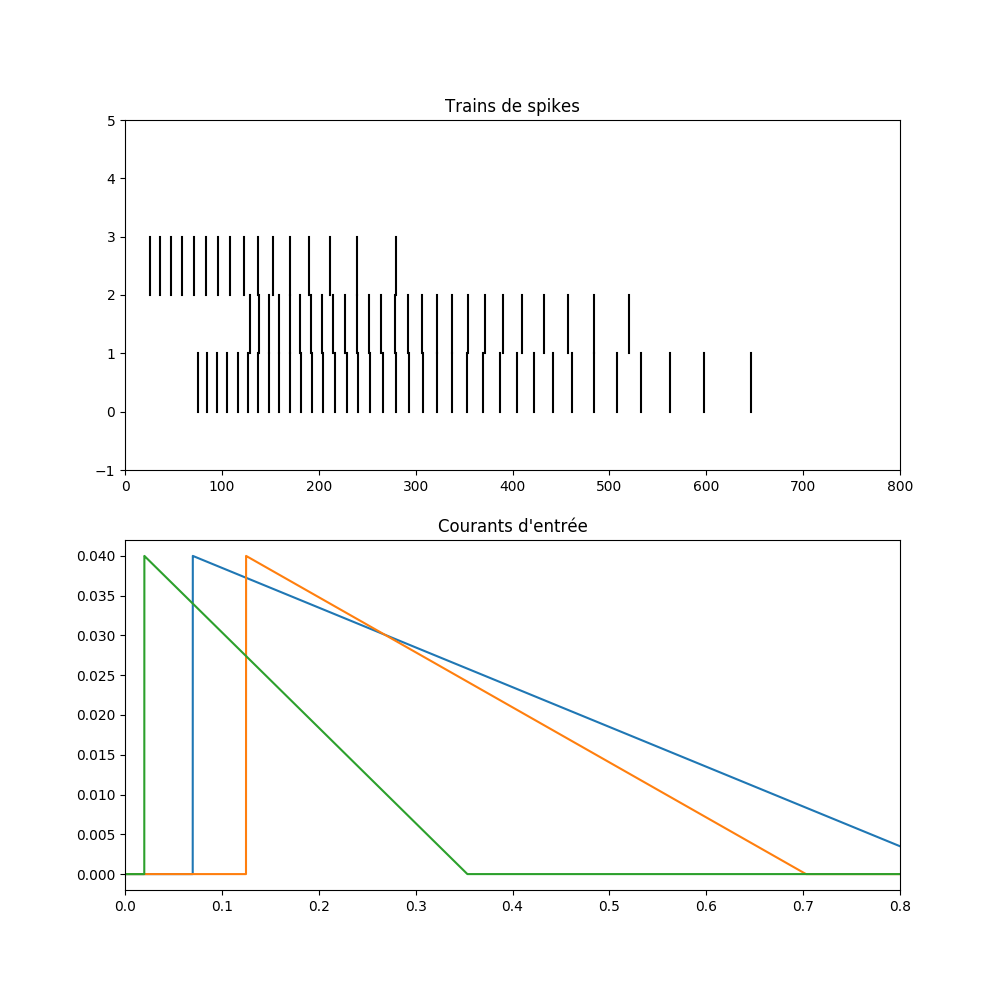
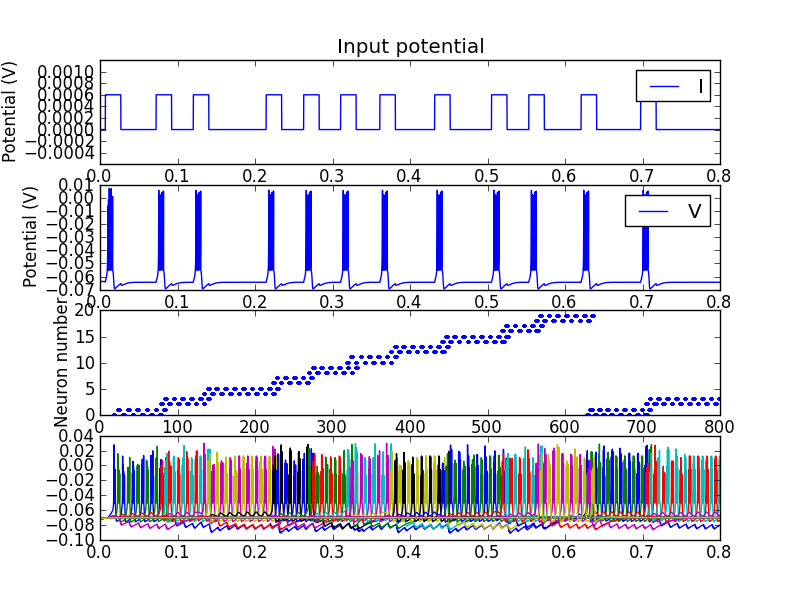
Q6 On se définiera un groupe de 3 neurones avec les paramètres habituels mais sans couplage dans un premier temps. Le courant d'entrée de ces trois neurones sera initialement nul puis suivra une rampe décroissante qui débutera respectivement aux temps 20ms, 70ms, 125ms. Ces rampes de courant partiront de 40mv. On s'arrangera pour que la rampe pour l'événement à 20ms décroisse avec une pente de 0.05mvolt ⁄ msecond. On ajustera les pentes de ces rampes pour que les trois rampes s'intersectent à 200ms. On simulera pendant 800 ms et on tracera les spikes ainsi que le potentiel de membrane et le courant d'entrée (avec des StateMonitor sur V et sur I). Cela devrait vous donner quelque chose comme ci-dessous. Vous remarquerez que les neurones ne sont jamais synchrones! Pour injecter un courant, on se réfèrera à l'annexe Injecter un courant .
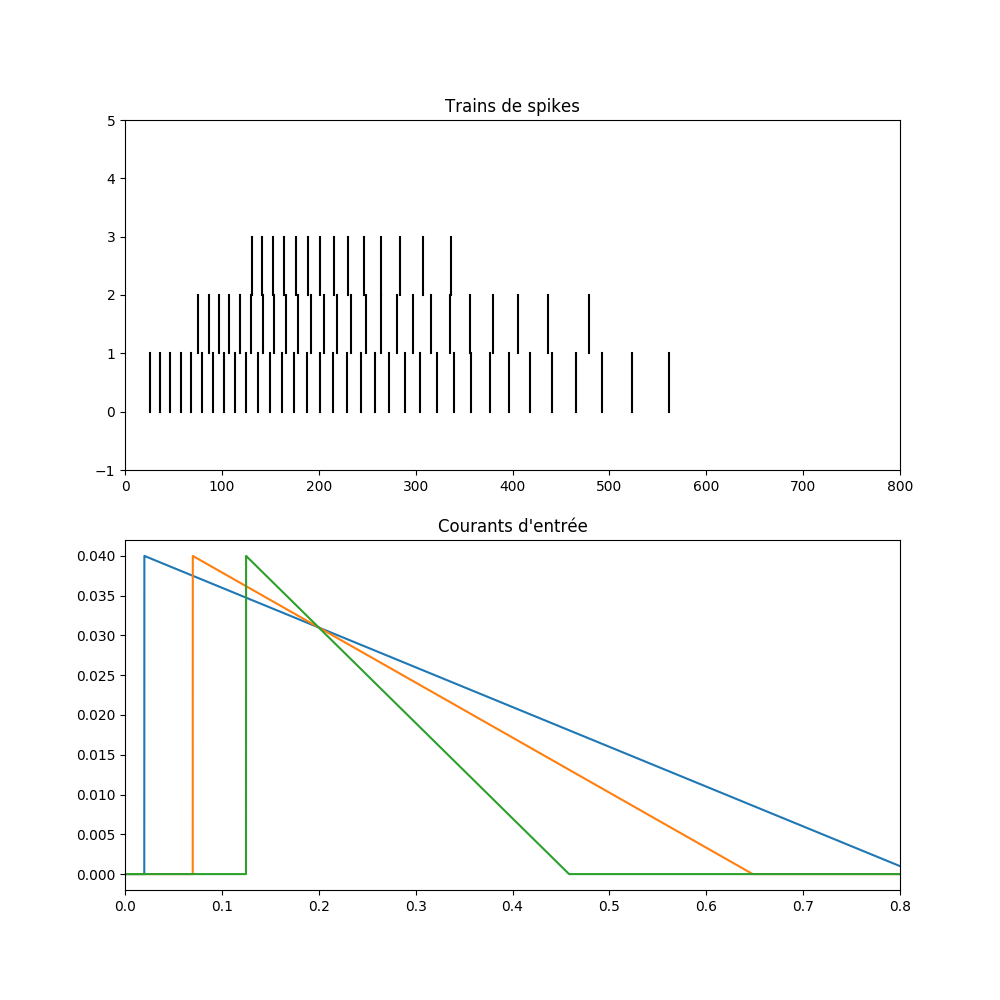
Q7 Introduisez maintenant un couplage excitateur de poids 0.7mV entre les neurones. Relancez la simulation et constatez qu'ils se synchronisent autour de 200ms.
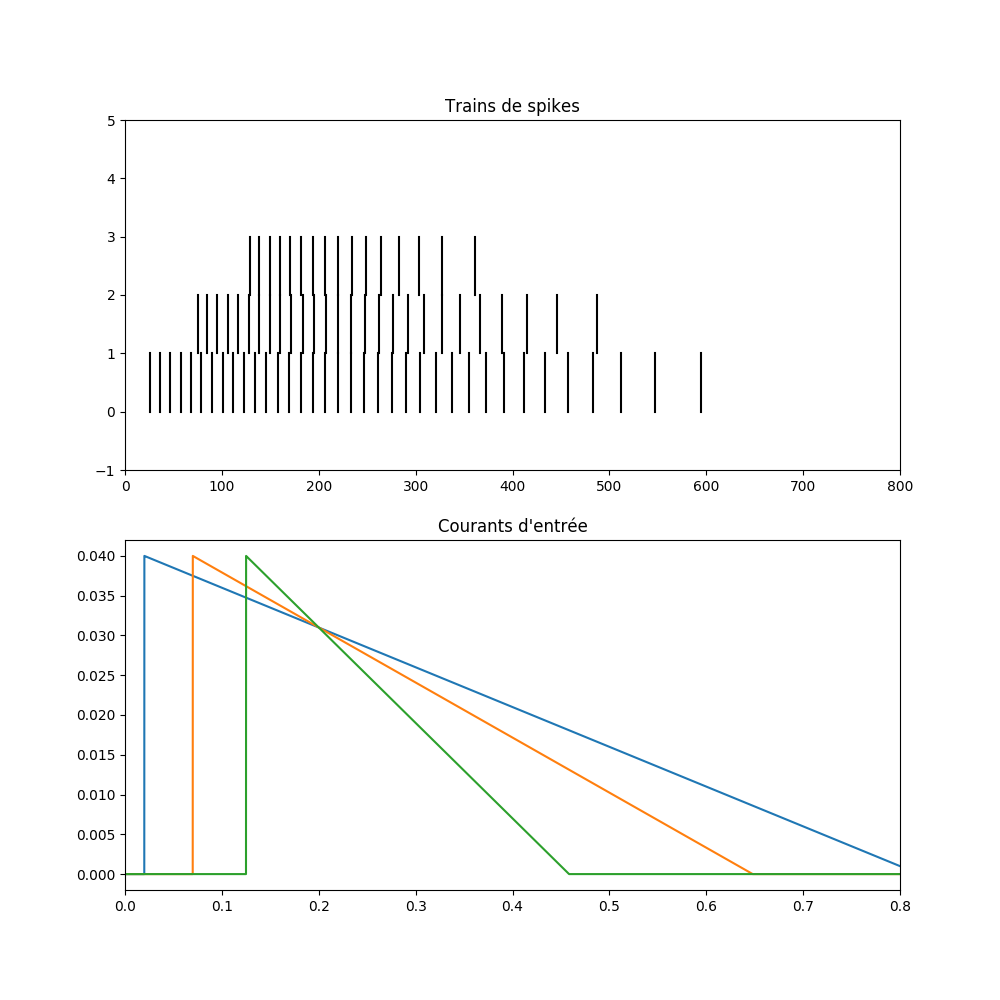
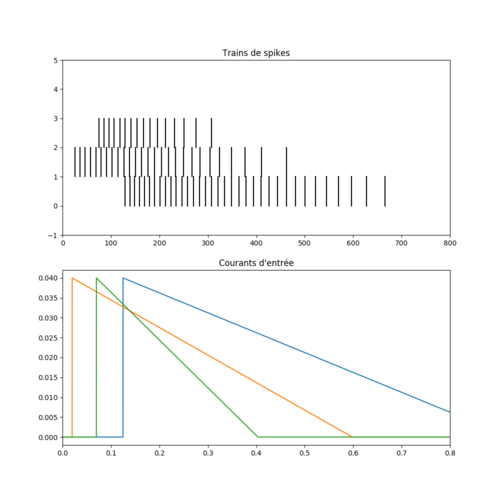
Q8 Enfin, en supposant que vous avez créé une liste ti qui contient les temps d'arrivée des événéments. De cette liste, vous avez déduit les pentes pour que les courants s'intersectent. Modifiez votre script pour qu'une fois que les pentes sont calculées, les temps d'arrivée des événéments soient permutés. On veut ici vérifier que les neurones ne se synchronisent pas si les événements n'arrivent pas dans le bon ordre. Vous devriez par example obtenir quelque chose comme ci-dessous.
Détecteurs de coïncidence
La couche chargée de reconnaitre l'occurence d'un mot fonctionne en détectant la coincidence de spikes de la couche en dessous. Un détecteur de coincidence peut se faire simplement à l'aide d'un intégrateur à fuite. On a vu que si un intégrateur à fuite n'est pas suffisamment stimulé dans une certaine fenêtre de temps, il ne va pas décharger. Au contraire, si il reçoit suffisamment d'excitation, il va décharger. Cette fenêtre de temps pendant laquelle il doit recevoir suffisamment d'excitation pour pouvoir décharger dépend des constantes de temps de l'intégrateur, de l'amplitude des spikes afférents, ...
Dans cette partie, on va tester expérimentalement la sensibilité d'un détecteur de coïncidence. On s'intéresse à un cas particulier ou un neurone doit détecter la coïncidence de 3 spikes. On suppose que chacun des spikes contribue également à la croissance du potentiel de membrane et on cherche une valeur pour cette contribution telle que le détecteur ait une certaine sensibilité temporelle. On se définit la sensibilité temporelle comme la durée td telle que si les trois spikes arrivent dans une fenêtre de temps inférieure à td, le neurone décharge et si les spikes arrivent dans une fenêtre de temps supérieure à td, le neurone ne décharge pas. On ne fera pas d'étude théorique (vous pouvez regarder dans le document Pourquoi ça marche ? Etude théorique ) mais on testera plusieurs valeurs de couplage et on concluera sur les paramètres qui assurent que notre détecteur de coïncidence fonctionne.
Pour pouvoir tester ce détecteur de coïncidence, il faut se mettre en place trois neurones qui génèrent l'entrée et un neurone pour détecter la coïncidence. On partira sur des neurones intègre et tire avec l'équation ci-dessous:
τ(dV)/(dt) = − (V − Vs) + I
si V ≥ Vt, alors V = Vr
avec τ = 5ms, Vt = − 55mV, Vs = − 65mV, Vr = − 75mV.
Préalablement D'après la question de la première partie, vous connaissez le temps d'émission d'un spike d'un neurone. Si on note V(0) = V0, on sait que le neurone émettra un spike au bout d'un temps t = τlog⎛⎝(V0 − (Vs + I0))/(Vt − (Vs + I0))⎞⎠. Déduisez en le courant à injecter I0 pour que le neurone décharge des spikes avec une période T ainsi que le potentiel de départ V0 pour que le premier spike arrive avec un déphasage donné. Les expressions que vous venez de trouver vont nous permettre de définir les courants d'excitation des neurones pour assurer que nos spikes arrivent exactement lorsqu'on le souhaite, ce qui va nous aider à tester notre détecteur de coïncidence.
Q9 Je vous propose qu'on écrive un script qui prenne en argument Δt1, Δt2, g (voir l'annexe Passer des arguments à un script Python) qui sont respectivement le temps entre le premier et le deuxième spike et le temps entre le premier et le troisième spike et l'amplitude de la connexion excitatrice entre les neurones d'entrée et le détecteur. Vous pouvez utiliser le script ex_coincidence.py comme point de départ.
On testera en particulier les conditions ci-dessous et on vérifiera en particulier si le neurone décharge bien un spike après la réception du troisième spike (i.e. il ne décharge pas après le deuxième spike et il décharge bien après le troisième).
- g = 4.1 mvolt , Δt2 = 3ms, Δt1 = 0.5ms, 1ms, 1.5ms, 3ms
- g = 6 mvolt, Δt2 = 3ms, Δt1 = 0.5ms, 1ms, 1.5ms, 3ms
- g = 4.85 mvolt, Δt2 = 3ms, Δt1 = 0.5ms, 1ms, 1.5ms, 3ms
- g = 4.85 mvolt, Δt2 = 4ms, Δt1 = 0.5ms, 1ms, 1.5ms, 3ms
Vous devriez pouvoir conclure qu'avec g = 4.85 mvolt, le neurone est un détecteur de coïncidence de 3 spikes dans une fenêtre de 3 ms. Pour des délais du dernier spike plus long, on ne peut pas garantir que le neurone va détecter les 3 spikes. La sensibilité peut être adaptée; par example, pour g=3.6 mvolt, on détecte des spikes dans une fenêtre de 0.5ms. Attention, si vous essayez avec ces valeurs, il est possible qu'il faille ajuster la constante de temps pour l'intégration de l'équation différentielle :
defaultclock.dt = 0.01*msecond
Connectons tout ensemble
On dispose maintenant de toutes les briques nécessaires pour fabriquer le modèle de Hopfield et Brody :
- déclencher des rampes décroissantes de courant à la détection d'un événément
- produire des trains de spikes avec des fréquences de décharge décroissantes associées aux courants d'entrée décroissants
- synchroniser de manière transitoire une population de neurones à spikes ayant des fréquences de décharge similaire
- détecter la synchronisation d'un ensemble de neurones à spikes
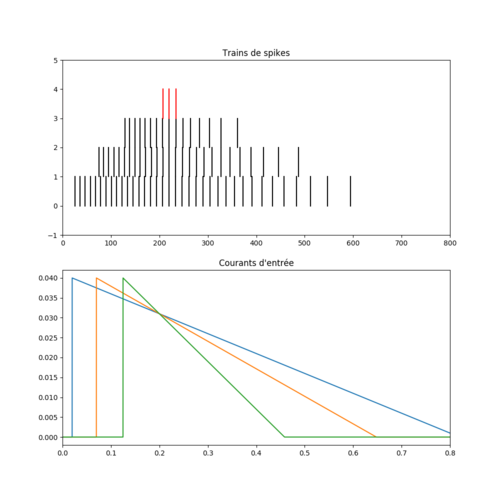
Q10 Il ne vous reste plus qu'à tout mettre ensemble pour finalement obtenir un neurone de sortie qui ne décharge que si la séquence de l'événement 1 présenté à 20ms, suivi de l'événement 2 présenté à 70 ms suivi de l'événement 3 présenté à 125 ms est présentée.
Pour le détecteur de coïncidence, vous aurez peut être besoin d'ajuster la constante de temps et le poids. J'ai pris τ = 2ms et g = 4.5mvolt pour l'image ci-dessous. Il peut aussi arriver que des synchronisations apparaissent par hasard quand vous permutez l'ordre des événéments. Je pense que cet effet se verrait moins si on utilisait une population plus importante.
Pour finir, les scripts utilisés pour résoudre les questions précédentes sont les suivants :
- Générer des spikes et prédire le temps inter-spikes ex1_correction.py
- Synchroniser une population de neurones à spikes ex3_correction.py
- Synchronisation transitoire ex6_correction.py
- Détecteur de coincidence ex9_correction.py
- Tout connecter tout_connecte.py
Pourquoi ça marche ? Etude théorique
On peut étudier théoriquement les conditions obtenir les propriétés que nous avons exploitées dans les parties précédentes. Dans le document study.pdf , j'étudie en partie ces propriétés, notamment:
- le modèle intègre et tire
- les conditions pour détecter la synchronie de 2 et 3 spikes
- quelques outils utilisés pour étudier la synchronisation d'oscillateurs couplés
Le modèle d'Izhikevic
Dans la partie précédente, vous avez mis en oeuvre un modèle très simple de neurones à spikes, le modèle intègre et tire à fuite. Le modèle intègre un courant constant (caché derrière le potentiel El) qui amène le potentiel du neurone vers un potentiel légèrement supérieur au potentiel de décharge. Il existe une grande variété de modèles qui permettent de rendre compte d'une plus ou moins grande variété de réponses de neurones enregistrées: des modèles simple comme le modèle intègre et tire mais qui ne permet pas d'exhiber une grande variété de réponse et des modèles plus compliqués comme le modèle d'Hudgkin-Huxley plus couteux à simuler mais aussi plus riche en termes de types de réponses qu'il peut exhiber. On va ici simuler le modèle d'Izhikevic . C'est un modèle relativement simple et qui permet d'exhiber différents types de réponses de neurones corticaux.
Le modèle d'Izhikevic, paramétré par quatre paramètres (a, b, c, d), est défini par les équations ci-dessous:
⎧⎨⎩ τ(dv)/(dt) = 0.04*103v2 + 5v + 140 − u + I τ(du)/(dt) = a(bv − u)
si v ≥ 30mV, alors⎧⎨⎩ v = c u = u + d
avec τ = 0.2ms. Attention, il faut préciser les unités de certaines constantes dans l'équation du modèle pour que ces unités soient cohérentes et l'équation acceptée par Brian. En particulier, on précisera 0.04*103* volt − 1 et 140* mvolt
En fonction des paramètres (a, b, c, d), on peut simuler:
- des neurones qui spikent de manière régulière
- des neurones qui émettent des bouffées soudaines de spikes, régulièrement
- des neurones qui émettent une bouffée de spikes à l'onset d'une stimulation
- ...
Simulez différentes réponses de neurones à spikes. Codez le modèle d'Izhikevic avec Brian et testez différentes valeurs des paramètres du modèle pour exhiber différentes comportements. On pourra essayer les valeurs suivantes :
- a = 0.02, b = 0.2, c = − 65mV, d = 6mV en injectant un courant I = 14mV
- a = 0.02, b = 0.2, c = − 55mV, d = 0.05mV en injectant un courant I = 0.6mV
Ce qui devrait vous donner des réponses comme le regular spiking et le chattering de la page d'Izhikevic;
Considérons maintenant qu'on ne cherche pas à simuler des neurones biologiques mais à assembler des neurones à spikes comme des briques de légo pour fabriquer une machine qui calcule. L'avantage du modèle d'Izhikevic est qu'avec une seule équation, on peut obtenir différents comportements. On peut par example détecter l'onset d'un stimulus, répondre tant qu'un stimulus est actif, etc...
Des neurones compteurs
On peut se construire un réseau de neurones à spikes à partir des deux types de neurones listés dans la partie précédente, les phasic bursting et tonic bursting, qui comptent le nombre de fois qu'une séquence d'entrée est à on. L'idée est que les phasic bursting détectent l'onset du stimulus et un réseau de tonic bursting se passent la main pour compter 1, 2, 3, ... modulo 10. Le modèle que je vous propose est représenté sur l'image ci-dessous, il ne vous reste plus qu'à le câbler et le simuler.
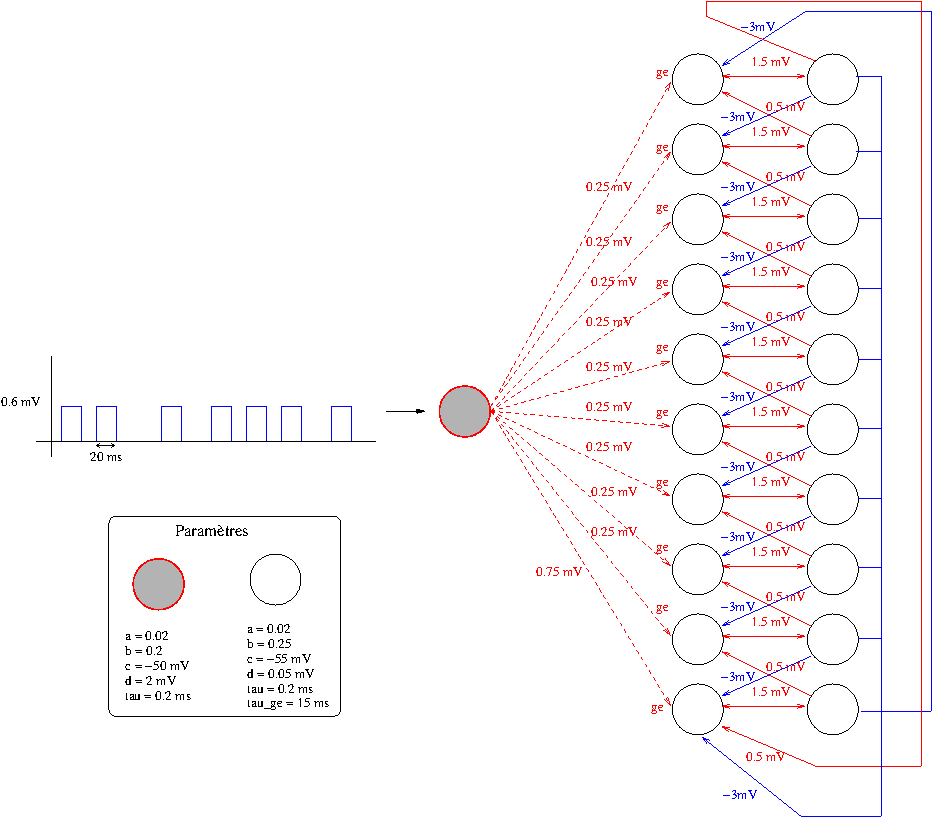
Une version avec une meilleure résolution du schéma est disponible : izhikevic_count.pdf . L'idée du circuit est de disposer d'un neurone détecteur d'onset qui va diffuser dans le reste du circuit le signal indiquant : j'ai détecté un tic d'horloge! Ce signal est phasique et uniquement délivré à la phase ascendante d'un créneau. Puis un ensemble de couples de neurones excitateurs/inhibiteurs va se passer la main. Le couple le plus en bas a une relation privilégiée avec l'entrée pour que le circuit puisse être mis en marche. Cette relation privilégée est inhibée si un des couples est excité (via l'inhibition de tous les neurones inhibiteurs vers le tout premier neurone excitateur en bas). Les connexions récurrentes excitatrices entre les neurones d'un couple assure un maintien d'activité. Au prochain tic d'horloge, plusieurs mécanismes se déclenchent. Comme le neurone inhibiteur du couple i excite le neurone excitateur du neurone i+1, la détection d'onset accompagnée de cette excitation permet d'exciter le neurone excitateur du couple suivant. Il reste ensuite à inhiber le circuit i pour qu'il passe effectivement la main. C'est le rôle de l'inhibition du couple i+1 vers le couple i. Important: toutes les projections excitatrices ciblent une conductance excitatrice ge et toutes les connexions inhibitrices ciblent une conductance inhibitrice gi. Ces conductances ont également une équation différentielle:
(dge)/(dt) = − ge ⁄ 15ms (dgi)/(dt) = − gi ⁄ 15ms (dv)/(dt) = (0.04.103v2 + .... − u + ge + gi) ⁄ τ
Cela devrait vous donner quelque chose comme :
Pour terminer cette partie, je vous donne les scripts que vous avez pu obtenir:
- Simuler le modèle d'Izhikevic izhikevic.py
- Compter avec des neurones à Spike izhikevic_count.py
Annexes
Table des matières
On fournit dans cette partie des bouts de code dont vous pourriez avoir besoin pour réaliser le TP;
Passer des arguments à un script Python
Pour passer des arguments à un script Python, il suffit d'utiliser le module sys. Il permet d'accéder à une liste sys.argv qui contient les arguments : nom_du_script <arg1> <arg2> ...
Fichier example_arguments.py
# -*- coding: utf-8 -*-
# J'importe le module sys pour accéder à la liste des arguments
import sys
# len(.) me retourne la taille d'une liste
if(len(sys.argv) != 2):
print("Utilisation : {} argument(float)".format(sys.argv[0]))
# Dans ce cas, je quitte le programme
sys.exit(-1)
# Je récupère le premier argument et le cast en float
arg1 = float(sys.argv[1])
# Et on l'affiche
print("Vous avez passé l'argument: {}".format(arg1))
Syntaxe d'une fonction en python
Fichier example_fonction.py
# -*- coding: utf-8 -*-
import numpy as np
import math
def ma_fonction(x,n):
# Note : Pas besoin de typer les arguments de la fonction en python
print("J'appelle ma fonction !")
y = np.array([math.pow(x,i)/math.factorial(i) for i in range(n)]).sum()
# Et je retourne un résultat, couple, etc... si j'ai besoin
return y
print(ma_fonction(1,10), np.exp(1))
Permuter les éléments d'une liste
Fichier example_shuffle.py
#!/bin/env python
# -*- coding: utf-8 -*-
import random
l = list(range(5))
print(l)
for i in range(5):
random.shuffle(l)
print(l)
Injecter un courant
La méthode la plus simple pour injecter un courant constant est de définir une variable dans les équations du modèle et d'initialiser cette variable à cette valeur constante. Pour chaque groupe, les variables internes (par example V, I, ..) qu'on définit sont des vecteurs de la taille du groupe dont on peut changer certaines composantes uniquement. On peut également utiliser la classe TimedArray pour spécifier des courants constants par morceaux. Ces trois cas sont illustrés dans le script ci-dessous.
Fichier example_courant_constant.py
#!/bin/env python
# -*- coding: utf-8 -*-
from brian2 import *
tau = 20 * msecond # constant de temps
Vt = -55 * mvolt # seuil pour spiker
Vr = -75 * mvolt # potentiel de reset
Vs = -65 * mvolt # potentiel de repos
eqs = '''
dV/dt = (-(V-Vs) + I)/tau : volt
I : volt
'''
G = NeuronGroup(N=10,
model=eqs,
threshold='V > Vt',
reset='V = Vr',
method='linear')
# On injecte un courant constant identique à tous les neurones
G.I = 10 * mvolt
# Ou on applique un courant constant différent par neurone
G.I[0] = 15 * mvolt
G.I[1] = 17 * mvolt
# Ou bien on change le courant à des instants déterminés
# en appelant la fonction update_input toutes les 20 ms ici
# c'est le décorateur @network_operation qui le permet
G.I = 0
@network_operation(dt=20*ms)
def update_input():
G.I = 15 * mV - G.I
# On monitor l'entrée, on lance la simulation et on plot l'entrée
statemon_input = StateMonitor(G, 'I', record=True)
run(200*ms)
figure()
plot(statemon_input.t, statemon_input.I.T)
show()
Une dernière façon de procéder est d'écrire une fonction, appelée systématiquement avant chaque itération et qui se charge de changer le courant.
Fichier example_courant_variable.py
#!/bin/env python
# -*- coding: utf-8 -*-
from brian2 import *
tau = 20 * msecond # constant de temps
Vt = -55 * mvolt # seuil pour spiker
Vr = -75 * mvolt # potentiel de reset
Vs = -65 * mvolt # potentiel de repos
eqs = '''
dV/dt = (-(V-Vs) + I)/tau : volt
I : volt
'''
G = NeuronGroup(N=10,
model=eqs,
threshold='V > Vt',
reset='V = Vr',
method='linear')
def get_currents(t):
if(t < 50 * ms):
return 0
else:
I = random(len(G))
# Pour montrer l'utilisation de where
# On annule toutes les valeurs plus grande
# que 0.75
I[where(I > 0.75)] = 0
return I
# Le décorateur network_operation(when='start')
# assure que la fonction set_current sera appelée
# à chaque itération
@network_operation(when='start')
def set_current():
global G
# On modifie les entrées du neurones
G.I = get_currents(defaultclock.t) * volt
statemon_input = StateMonitor(G, 'I', record=True)
run(100 * ms)
figure()
plot(statemon_input.t , statemon_input.I.T)
show()
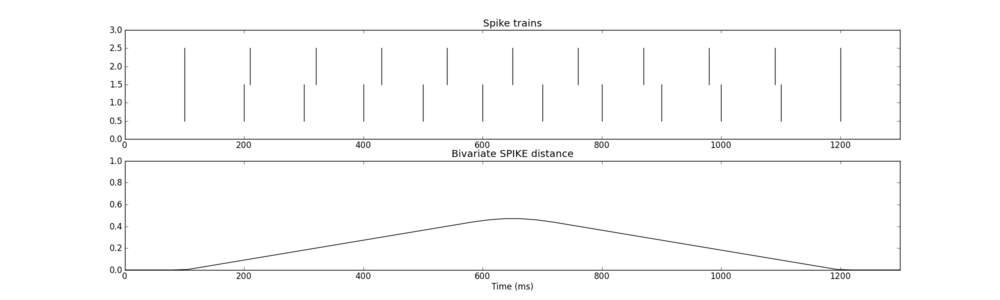
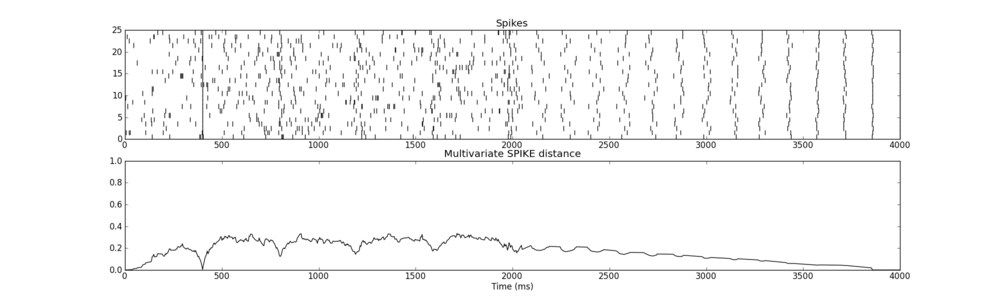
Mesurer la synchronie d'une population de neurones
Pour mesurer la synchronie d'une population de neurones à spikes, on utilisera la mesure de Kreuz(2012) . Pour ce faire on copiera le script spike_distance.py dans le répertoire dans lequel on exécute la simulation et on utilisera un code de la forme suivante :
Fichier example_synchronie.py
# -*- coding: utf-8 -*-
from brian import *
from spike_distance import *
N = 10 # On simule 10 neurones
........
# On monitore les spikes de nos neurones
spikemon = SpikeMonitor(G)
# On se construit une liste des tableaux des temps de spikes
#
list_spike_trains = []
[list_spike_trains.append(spikemon[i]) for i in range(N)]
# On suppose que la simulation se déroule entre 0 et tmax
# et on considère 100 points sur lesquels la distance est calculée
t, Sb = multivariate_spike_distance(list_spike_trains, 0, tmax/second, 100)
# On trace ensuite la distance
figure()
plot(t, Sb)
show()
Vous voyez ci-dessous des examples de ce que donne ces mesures. La mesure est toujours normalisée entre 0 et 1. Une distance de 0 indique une parfaite synchronie.